因为本人在 whk,所以写的很慢。
受篇幅约束,本人主要讲解实现,关于 TB5 分治在该问题约束下最优性的证明请参考 lxl 原 PPT。
参考自 清华大学 李欣隆 的 PPT《范围修改查询问题》。
请注意,TB5 分治最优秀的地方在于操作次数的最优化,关于时间复杂度其实不见得是很好的做法。
目录
信息的基本分类及范围的概念
双半群模型——范围修改查询问题的抽象数据结构模型
平面图点定位
TB5 分治——最优操作次数离线范围修改查询算法
半平面模型及其例题
信息的基本分类及范围的概念
半群
给定一个集合 $D$ 以及一个集合 $D$ 上的二元运算 $\times$ 满足 $D \times D \rightarrow D$。
对于该运算满足结合律:$a,b,c \in D,(a \times b)\times c = a \times (b \times c)$。
幺半群
给定一个集合 $D$ 以及一个集合 $D$ 上的二元运算 $\times$ 满足 $D \times D \rightarrow D$。
对于该运算满足结合律:$a,b,c \in D,(a \times b)\times c = a \times (b \times c)$。
满足幺元存在使得:$a,\epsilon \in D,a \times \epsilon = \epsilon \times a = a$。
交换半群
给定一个集合 $D$ 以及一个集合 $D$ 上的二元运算 $\times$ 满足 $D \times D \rightarrow D$。
对于该运算满足结合律:$a,b,c \in D,(a \times b)\times c = a \times (b \times c)$。
对于该运算满足交换律:$a,b,c \in D,a \times b = b \times a$。
范围
常见的范围有序列区间,树简单路径,二维平面矩形,高维正交范围,半平面范围,圆范围。
我们一般理解成对于进行修改和查询的信息的限制。
双半群模型——范围修改查询问题的抽象数据结构模型
受不了了,不想自己写。
直接贺一下 lxl PPT 里的图。

还需要注意的是对于 $D \times M \rightarrow D$ 的 $\times$ 运算对于 $(D,+)$ 运算具有分配律。
我们称这样的模型为双半群模型。
平面图点定位
我应该会讲一下这玩意儿。因为我现在还不会。
网上资料学不懂,等我再复习一下计算几何。
TB5 分治——最优操作次数离线范围修改查询算法
其实最重要的,这玩意儿严格以上来说应该是最优操作次数。
等价类
我们先来看一个简单的题,对于长为 $n$ 的序列做区间加区间和 $m$ 次。
这个太简单了,练习时长两年半的学生都会用线段树做 $O(n + m \log n)$。
但是如果 $m$ 很小呢?我们考虑一种 $O(n + m \log m)$ 的做法,考虑将共 $2m$ 个端点离线下来,我们发现中间的空隙段可以被整合成一个合并的信息进行维护,因为它们时时刻刻都被整体修改查询,然后对于 $O(m)$ 个点用线段树,时间复杂度 $O(n + m \log m)$。
那么在一定的操作下能被划分成满足“时时刻刻都是被整体修改查询”的信息集合我们可以称其为等价类。
我们记 $R_{l,r}(x,y) = [\forall i \in [l,r],x \in q_i \wedge y \in q_i]$,即任意两点 $x,y$ 在第 $l \sim r$ 个操作中是否属于“被整体修改查询”。
显然对于 $[l',r'] \in [l,r]$,任意的 $R_{l,r}(x,y) \rightarrow R_{l',r'}(x,y)$,因为操作越多划分更细,所以显然的是若 $R_{l,r}(x,y) = 1$ 那么对于任意的 $R_{l',r'}(x,y) = 1$,上面的箭头即一个 DAG 型的取或传递关系。
在进行划分的时候我们一个想法是尽量能少划分就少划分以达成减少数据结构需要维护的信息数量。
不难发现操作越多,划分的越细。
从 lxl 的 PPT 里面扒了个例子下来,如图,划分的范围是双曲线,相应的等价类在图中已标明。
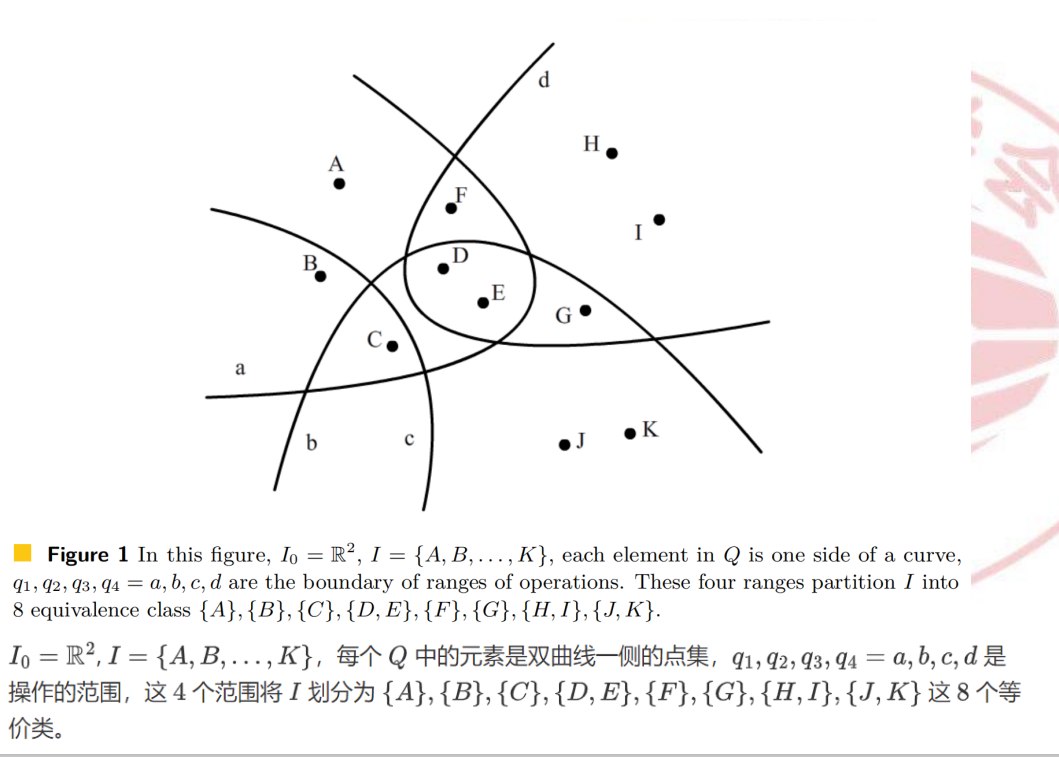
动态有根森林
下文假设所有对于分治数据结构上节点的信息修改都是 $O(1)$ 数量级的。即我们的操作次数。
联想到我们树形分治数据结构的本质思想:叶子层节点是我们实际需要维护的信息,非叶子层节点的建立是为了方便修改和查询而建立的辅助节点。
我们常用且在大多数时比较高效的数据结构:线段树。它的一些性质:
符合树形分治数据结构的本质思想;
每个节点上有子树中所包含的叶子节点信息和,以及负责下传的标记;
二叉;
树高 $O(\log n)$;
节点数量级为 $O(n)$。
所以我们考虑维护这样一个动态有根森林,满足:
动态森林的每棵树都对应一个等价类;
符合分治树形分治数据结构的本质思想;
每个节点上有子树中所包含的叶子节点信息和,以及负责下传的标记;
对于非叶子节点的叉数不固定;
节点数量级为 $O(n)$。
我们贪心地想要让等价类的数量更少,即让我们的划分符合等价类定义的情况下划分的更粗点。
如何在加操作和删操作时维护动态有根森林
我们的想法很直接,动态地维护加点和删点。
离线所有操作,记操作序列为 $q$,长为 $p$。
在维护时由于合并等价类看起来更容易些,即删操作更容易些,所以考虑线段树分治,我们维护出最开始的操作 $\{q_1,q_2,\dots,q_p\}$ 都存在时的动态有根森林是长什么样子的。
每次走到线段树上一个节点 $[l,r]$,代表着当前 $\{q_l,q_{l+1},\dots,q_r\}$ 操作下动态树森林的样子。从 $[l,r] \rightarrow [l,\text{mid}]$ 时,我们暴力合并当前需要合并的等价类(即将涉及到的等价类对应的树根绑在一个新开的点上)相应地更新一下新开节点的信息。
当走到叶子节点时,不难发现只存在 $O(1)$ 个等价类,即森林大小为 $O(1)$,此时我们找到我们需要修改/查询的等价类信息,就在对应的树根上进行 $O(1)$ 修改或者 $O(1)$ 查询。
从 $[l,mid] \rightarrow [l,r]$ 的回溯也很简单,你开个栈回退就行了,注意此时肯定只有删除节点,需要将被删除节点的标记下传到连接的儿子上,并且我们发现此时只会删除根(你修改时都只会合并出来根回退时肯定也是删根),所以无需担心在查询时会出现之前祖先节点的标记信息没有下传到位的一系列奇怪现象。
从 $[l,r] \rightarrow [\text{mid + 1},r]$ 直接画葫芦就好了。
你会发现上述的过程无异于套了个分治然后暴力维护,太优雅了。但是时间复杂度看起来很爆炸啊!!!
下文会证明这一系列操作的时间复杂度,已知的是只和范围的维度有关系。
区域数
我们暂且先假设“找到需要合并的等价类树根”是 $O(1)$ 的。
定义离散函数 $F(k)$ 表示有 $k$ 个范围操作的情况下,在当前问题下最多能将所有信息划分为多少个等价类,设当前的信息一共有 $n$ 个,则实际上我们能将信息划分的最大等价类数量为 $\min(F(k),n)$。
同时定义离散函数 $G(k)=x$ 满足 $F(x) \leq n,F(x + 1) > n$ 。
以区间加区间和举例,在从 $[l,r] \rightarrow [l,\text{mid}]$ 的过程中,我们不妨设等价类的数量级与操作数数量级同级(显然端点个数数量级),那么每次看似“暴力”的从 $[l,r]$ 转移到 $[l,\text{mid}],[\text{mid},r]$ 的过程实际上只会涉及至多 $F(\text{len}) - F(\frac{\text{len}}{2})$ 个等价类的合并。
显然回退时间复杂度与合并时间复杂度是同数量级的,所以可以默认从一个父亲转移到另一个子节点单次涉及到的等价类合并数量级为 $O(F(\text{len}))$。
由此我们对该分治方法得到一个关于时间复杂度的计算方法:
$T_1(m) = 2T_1(\frac{m}{2}) + O(F(m))$。
对于具体问题运用主定理可以得到更为简洁的时间复杂度表现形式。
操作分块
观察到当维度很高的时候,例如做二维的一个矩形加矩形和之类的,对于 $c$ 维问题有 $F(m) = m ^ c$。
所以有时候得考虑对操作分块,以二维的范围修改查询问题举例,我们取阈值 $B = G(n) = \sqrt n$ 进行分块处理每个操作,时间复杂度计算如下:
$T = O(n) + \frac{q}{G(n)}T_1(G(n)),T_1(m) = 2T_1(\frac{m}{2}) + O(F(m))$
代入主定理,不难得到最后的时间复杂度为 $O(n + q \sqrt n)$ 的。
关于“找到需要合并的等价类树根”的方法
对于二维以上的问题我不会。
对于二维可以通过平面图点定位的方法,对于“找到需要合并的等价类树根”可以多消耗一只 $O(\log n)$ 来预处理得到和上文完全相同的做法。
但是对于一些一维问题如区间加区间和貌似是可以有更精巧的预处理方法。没必要强加一只 $O(\log n)$。
upd on 2023/1/11
和超人学者进行了深入交流,爷会了!
我们通常认为,我们采用如下的方法,进行“从一层节点的等价类向另一层的等价类建立相邻层映射”的过程:
将上一层的等价类视为可被修改的信息节点,从每个等价类内选择一个代表元执行操作;
通过可以实现的平凡数据结构,利用 hash,将下一层的修改操作对信息节点群执行范围加;
最后对每个点求和的过程,我们的问题从“范围修改查询”转化成了“范围修改,单点查询”,问了下 ccz,这样的问题转化大多数时会对问题降维,比如 P6109。
这里举几个例子。区间加区间和的通用方式就是使用区间加区间和线段树;矩形加矩形和的通用方法是扫描线加线段树;半平面修改查询的通用方法是四分树套旋转扫描线。
半平面修改查询通用方法
这个很重要。
我们建立的四分树不是传统意义上的二维线段树,我们假设我们就做半平面修改半平面查询,我们每次将一个平面按照点集大小均匀划分成四等份,任意一个半平面只会递归入至多三个平面,那么直接做“半平面修改查询”问题,时间复杂度 $T(n) = 3T(\frac{n}{4})$ 可解得 $T(n) = n ^ {0.79}$。
如果是“半平面修改,单点查询”我们将底层换成旋转扫描线即可,钦定当四分树上区域内的点集大小小于等于 $x$ 时就开始做旋转扫描线。
设当前等价类的个数为 $n$,操作次数为 $m$。除了在四分树上的标记,我们在底层的半平面修改全都需要旋转扫描线,直接定位和修改即可。
四分树:$m(\frac{n}{x})^{0.79}\log n$。
旋转扫描线:$nx \log n$。
平衡一下就可以做到 $n ^ {1.44} \log n$,只是我平衡出来好像是 1.66 还是多少,也许是算错了。
实例代码
线段树区间加区间和板子,初始化预处理出来底层等价类,每次选择等价类中的一个点设为代表然后用 hash 对每层“范围修改,单点查询”,开栈回撤即可。
事实上可以通过合并离散化端点的方式来合并等价类,时间复杂度就可以砍一个 $O(\log n)$。
范围查询和范围修改查询区别
只有查询基本上时间复杂度和操作数有关;而范围修改查询就不一样。
一个好的例子是区间加区间和如果操作数为 $m = n ^ 2$,那我们直接暴力预处理所有可能询问即可。
实际应用
[CTS2021]测测你的半平面修改查询
暂时没被公开,虽然在 PPT 内算是被公开了但是还是先不讲了。
其实就是将上面的二维问题换成了半平面。
卡 KDT 修改次数的常
这个是矩形操作的哈。
具体讲解,咕咕咕。
萌新的眼神.jpg。
半平面模型及其例题
这个在近几年的 Ynoi 中出现还是有那么几道。
主要思想有沿用等价类思想操作分块后旋转扫描线,以及基于随机撒点的半平面莫队等等。
随机数据半平面数点
由于点在平面上均匀随机分布,我们直接将平面剖成 $n$ 个 $\sqrt n \times \sqrt n$ 的小矩形,维护块后缀和,那么我们期望每个块内只有常数个点,即暴力处理 $\sqrt n$ 个散块和 $\sqrt n$ 个后缀块和即可。
旋转扫描线解决半平面问题

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号